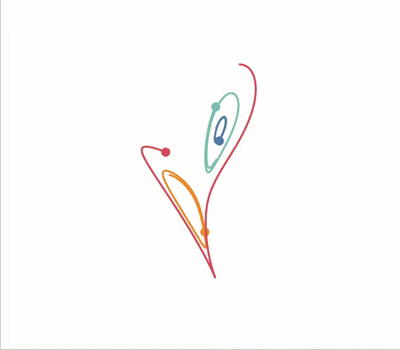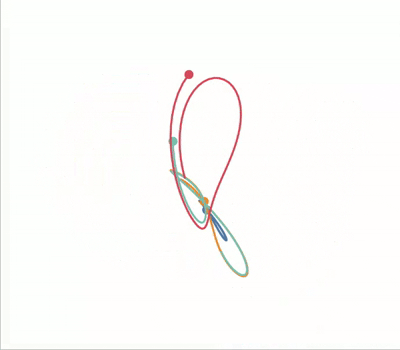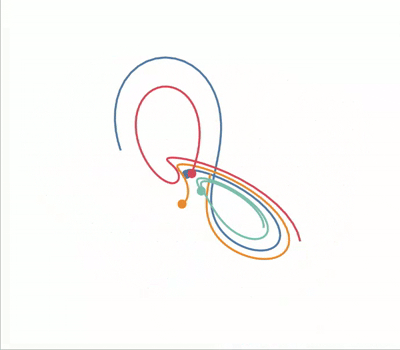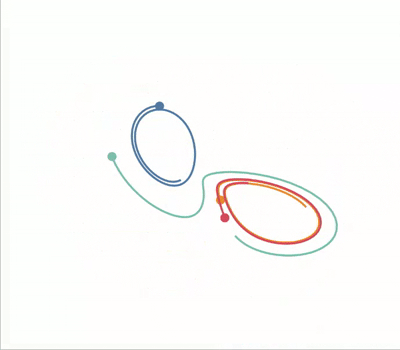The Lorenz Attractor

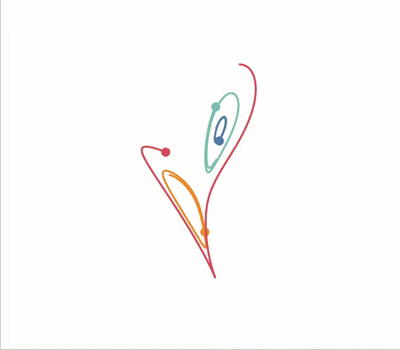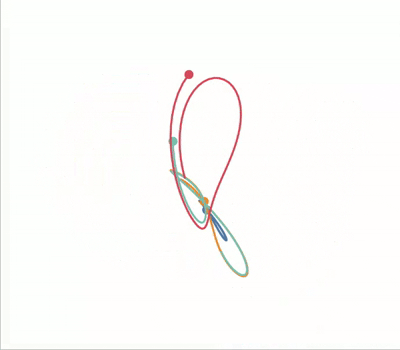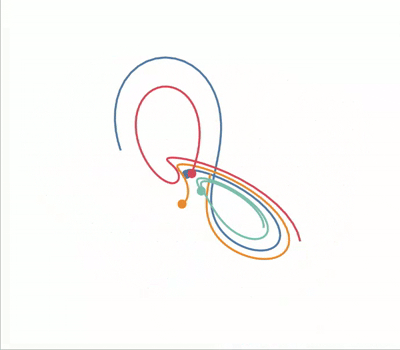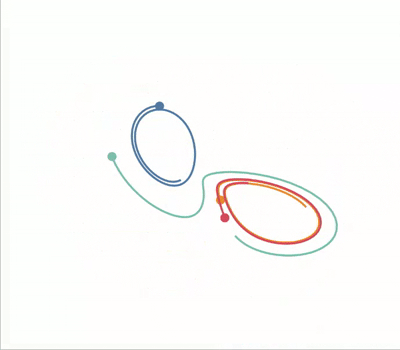
$\newcommand{\dd}{\mathrm{d}}$

The Lorenz system is a classic example of chaos in dynaimical systems. It’s known for its butterfly-shaped attractor and is defined by the following set of ordinary differential equations:

\[\frac{\dd x}{\dd t}=\sigma(y-x)\] \[\frac{\dd y}{\dd t}=x(\rho-z)-y\] \[\frac{\dd z}{\dd t}=xy-\beta z\]

Because of its striking visual when plotted it’ll serve as a good example to show how the animplotlib package can be used for creating a more complex animation in both 2D and 3D.

First ensure the animplotlib package is installed:

pip install animplotlib

We’ll make use of scipy.integrate.odeint to solve the system to generate the data being plotted. First we import the necessary libraries and define the attractor:

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from animplotlib import AnimPlot # AnimPlot class used for 2D animations

# parameters and initial conditions
sigma = 10
rho = 28
beta = 8/3
x0 = [0, 1, 15] # initial conditions
t = np.linspace(0, 100, 10000)

# defining the lorenz system
def lorenz(x_var, t):
    x, y, z = x_var
    dx_dt = sigma * (y - x)
    dy_dt = x * (rho - z) - y
    dz_dt = x * y - beta * z
    return [dx_dt, dy_dt, dz_dt]


# solving the system
x_solve = odeint(lorenz, x0, t)
x = x_solve[:, 0]
y = x_solve[:, 1]
z = x_solve[:, 2]

2D Animation

Let’s visualize the Lorenz attractor in three 2D projections: x vs y, x vs z, and y vs z.

fig, axs = plt.subplots(1, 3, figsize=(15, 5))

lines = []
points = []
xs = []
ys = []

# x vs y
line1, = axs[0].plot([], [], lw=0.5)
point1, = axs[0].plot([], [], 'ro', markersize=4)
axs[0].set_xlim(np.min(x), np.max(x))
axs[0].set_ylim(np.min(y), np.max(y))
axs[0].set_title('x vs y')
axs[0].set_axis_off()
lines.append(line1)
points.append(point1)
xs.append(x)
ys.append(y)

# x vs z
line2, = axs[1].plot([], [], lw=0.5)
point2, = axs[1].plot([], [], 'ro', markersize=4)
axs[1].set_xlim(np.min(x), np.max(x))
axs[1].set_ylim(np.min(z), np.max(z))
axs[1].set_title('x vs z')
axs[1].set_axis_off()
lines.append(line2)
points.append(point2)
xs.append(x)
ys.append(z)

# y vs z
line3, = axs[2].plot([], [], lw=0.5)
point3, = axs[2].plot([], [], 'ro', markersize=4)
axs[2].set_xlim(np.min(y), np.max(y))
axs[2].set_ylim(np.min(z), np.max(z))
axs[2].set_title('y vs z')
axs[2].set_axis_off()
lines.append(line3)
points.append(point3)
xs.append(y)
ys.append(z)

# Call the AnimPlot class
AnimPlot(fig, lines, points, xs, ys, plot_speed=2, l_num=1000)

3D Animation

To better see how these projections relate to each other we can create an animation in 3D using the AnimPlot3D class. Using the same code as above to solve the Lorenz system and generate the data:

fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d') # for 3D plotting
line, = ax.plot([], [], [], lw=0.5)
point, = ax.plot([], [], [], 'ro', markersize=4)
ax.set_xlim(np.min(x), np.max(x))
ax.set_ylim(np.min(y), np.max(y))
ax.set_zlim(np.min(z), np.max(z))
ax.set_title('3D Lorenz Attractor')
ax.set_axis_off()

anim.AnimPlot3D(fig, ax, line, point, x, y, z, plot_speed=2,
                rotation_speed=0.25, l_num=1000, blit=False)

A standout property of chaotic systems is that they are very sensitive to change in their input parameters. We can visualise this by plotting the Lorenz attractor with various initial conditions on the same axes:

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from animplotlib import AnimPlot3D

def lorenz_deriv(state, t, sigma=10, rho=28, beta=8/3):
    x, y, z = state
    dxdt = sigma * (y - x)
    dydt = x * (rho - z) - y
    dzdt = x * y - beta * z
    return [dxdt, dydt, dzdt]

def lorenz_trajectory(x0, y0, z0, t_step=5000, dt=0.01):
    t = np.linspace(0, t_step*dt, t_step)
    initial_state = [x0, y0, z0]
    states = odeint(lorenz_deriv, initial_state, t)
    xs, ys, zs = states[:,0], states[:,1], states[:,2]
    return xs, ys, zs

# Varying initial conditions
initial_conditions = [
    (0., 1., 1.05),
    (15., 10., 20.),
    (-15., -10., 30.),
    (5., -20., 40.)
]
# Colour values for each plot
colors = [
    "#4E79A7",
    "#F28E2B",
    "#76B7B2",
    "#E15759"
]

fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111, projection='3d')
ax.set_axis_off()

lines = []
points = []
xs, ys, zs = [], [], []

for ic, color in zip(initial_conditions, colors):
    x, y, z = lorenz_trajectory(*ic)
    xs.append(x)
    ys.append(y)
    zs.append(z)
    line, = ax.plot([], [], [], lw=2, color=color)
    point, = ax.plot([], [], [], 'o', color=color, markersize=8)
    lines.append(line)
    points.append(point)

ax.set_xlim(np.min(xs), np.max(xs))
ax.set_ylim(np.min(ys), np.max(ys))
ax.set_zlim(np.min(zs), np.max(zs))

AnimPlot3D(fig, [ax] * len(lines), lines, points, xs, ys, zs, plot_speed=2,
           rotation_speed=0.25, l_num=100, p_num=1)

Written on