Deriving expressions to model the relation between photosynthetic rate and light intensity in microalgae.

---

My masters research revolved around modelling microalgae growth in order to investigate how their growth could be optimised for CO₂ utilisation, post carbon capture. As microalgae are photoautotrophic, light plays a key role in their photosynthetic activity. A category of models which aim to account for light intensity are known as ‘P-I’ (photosynthetic rate and light intensity) relationships. These models, as the name suggests, model photosynthetic rate as a function of light intensity. The P-I relationship consists of three distinct regimes: light-limited, light-saturated and light-inhibited.

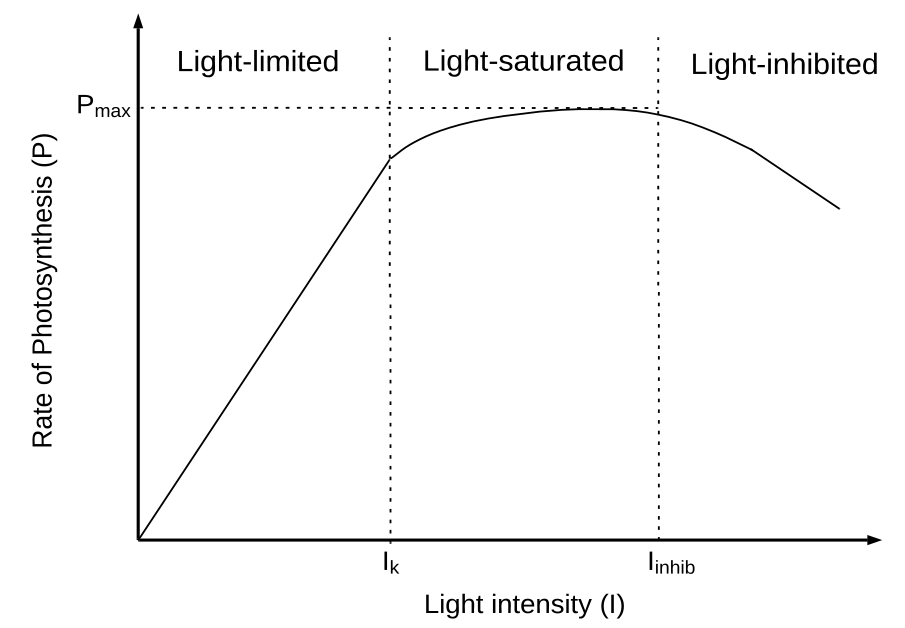
At low light intensities, the rate of photosynthesis is linear with light intensity, as photosynthesis is limited by the capture of photons (Béchet, et al., 2013). At $I_{k}$ the light intensity reaches a saturation threshold and the microalgae become light saturated. At this point, the rate of photosynthesis is limited by the rate of photosynthesis reaction. Photosynthetic rate reaches a maximum during this phase and becomes independent of light intensity. Past a certain inhibitory threshold essential enzymes involved in photosynthesis become denatured and the rate of photosynthesis begins to decrease, represented by $I_{inhib}$.

When modelling this relationship the following conditions must be satisfied:

$\newcommand{\dd}{\mathrm{d}}$ $\qquad \qquad \qquad Condition\;1$

\[When \ \ P = 0, \ \frac{\dd P}{\dd I} = \frac{P_m}{I_k}\]

$\qquad \qquad \qquad Condition\;2$

\[\lim_{P \to P_m} \frac{\dd P}{\dd I} = 0\]

$\qquad \qquad \qquad Condition\;3$

\[When \ I = 0, \ P = 0\]

$\qquad \qquad \qquad Condition\;4$

\[For \ \ 0 < P < P_m, \ 0 < \frac{\dd P}{\dd I} < \frac{P_m}{I_k}\]

where $P_{m}$ is the maximum photosynthetic rate. Early research into these types of models in the 70’s suggested a hyperbolic tangential relation between $P$ and $I$ (Chalker, 1979). In general, we can say that the relation between rate of photosynthesis and light intensity is of the form

\[\frac{\dd P}{\dd I} = f(P).\]

Expanding $f(P)$ out into a Maclaurin series expansion gives

\[\frac{\dd P}{\dd I} = a_{0} + a_{1}P + a_{2}P^{2} + a_{3}P^{3} \ldots.\]

We can derive various expressions using an increasing number of terms from the series expansion. From Condition 1, $P = 0, \ \frac{\dd P}{\dd I} = \frac{P_{m}}{I_{k}}$, we can see that $a_{0} = \frac{P_{m}}{I_{k}}$. Taking the first two terms,

\[\frac{\dd P}{\dd I} = \frac{P_{m}}{I_{k}} + a_{1}P,\]

and applying Condition 2 gives $a_{1} = - \frac{1}{I_{k}}$. And so we get

\[\frac{\dd P}{\dd I} = \left( \frac{1}{I_{k}} \right) (P_{m} - P).\]

For convenience, let us define $\alpha = \frac{1}{I_{k}}$. Integrating and solving for $P$ gives:

\[\frac{\dd P}{\dd I} = \alpha(P_{m} - P),\] \[\alpha \int \dd I = \int \frac{\dd P}{P_{m} - P},\] \[\alpha I = - \ln(P_{m} - P) + C.\]

Using Condition 3 we find that $C = \ln P_{m}$. And so, after rearranging, we get a simplified expression relating $P$ and $I$:

\[\alpha I = \ln \frac{P_{m}}{P_{m} - P},\] \[e^{\alpha I} = \frac{P_{m}}{P_{m} - P},\] \[P_{m} - P = \frac{P_{m}}{e^{\alpha I}},\] \[P = P_{m}(1 - e^{-\alpha I}).\]

Though is a simple expression, it hasn’t been found to fit experimental data particularly well (Kurano and Miyachi, 2005). If we instead start with the first three terms,

\[\frac{\dd P}{\dd I} = \frac{P_{m}}{I_{k}} + a_{1}P + a_{2}P^{2},\]

from Condition 2 we get that $a_{1} = -(\alpha + a_{2}P_{m})$. Therefore,

\[\begin{align*} \frac{\dd P}{\dd I} &= P_{m}\alpha - (\alpha + a_{2}P_{m})P + a_{2}P^{2}, \\ &=P_{m}\alpha - \alpha P - a_{2}P_{m}P + a_{2}P^{2}, \\ &= \alpha(P_{m} - P) - a_{2}P(P_{m} - P). \end{align*}\]

Integrating and solving for $P$ gives

\[\left[ 1 - \left( \frac{P_{m}a_{2}}{\alpha} \right) \right] \alpha I = \ln \left[ \frac{P_{m} - \left( \frac{P_{m}a_{2}}{\alpha} \right) P}{P_{m} - P} \right],\] \[P = P_{m}\left[ \frac{\exp\left[\alpha I\left(1 - \frac{P_{m}a_{2}}{\alpha}\right)\right] - 1}{\exp\left[\alpha I \left( 1 - \frac{P_{m}a_{2}}{\alpha} \right) \right] - \left( \frac{P_{m}a_{2}}{\alpha} \right) } \right].\]

Hyperbolic tangent expression

Setting the derivative of $\frac{\dd P}{\dd I}$ equal to zero, we can find that the maximum slope occurs at $P = \frac{\alpha + a_{2}P_{m}}{2a_{2}} = \frac{-a_{1}}{2a_{2}}$. And so, the maximum slope can be given by

\[\left( \frac{\dd P}{\dd I} \right)_{max} = \alpha P_{m} + \frac{a_{1}^{2}P_{m}}{4(\alpha + a_{1)}}.\]

For the sake of convenience, let $\epsilon = - \frac{P_{m}a_{2}}{\alpha}$. The expression for $P$, thus, becomes

\[P = P_{m} \left[ \frac{e^{\alpha I(1+\epsilon)} - 1}{e^{\alpha I(1+\epsilon)} - \epsilon} \right].\]

From Conditions 1 and Conditions 2 we get that the initial slope is $\alpha P_{m}$, and that this value decreases as $P$ increases. As the slope can only exceed this for negative values of $P$ and $I$, which have no biological meaning, it must be that the maximum possible slope is $\alpha P_{m}$. We can see from the expression for maximum slope that it will exceed $\alpha P_{m}$, except for when $a_{1} = 0$. When this is the case, $a_{2} = - \frac{\alpha}{P_{m}}$ and $\epsilon = 1$. We can, therefore, write the equation for $\frac{\dd P}{\dd I}$ we defined above as

\[\frac{\dd P}{\dd I} = \alpha(P_{m} - P)\left( 1 + \frac{P}{P_{m}} \right).\]

And so, integrating and rearranging for $P$ gives the hyperbolic tangent relation:

\[2\alpha I = \ln \left( \frac{P_{m} + P}{P_{m} - P} \right),\] \[P = P_{m}\left( \frac{e^{2\alpha I} - 1}{e^{2\alpha I} + 1} \right) ,\] \[P = P_{m} \tanh (\alpha I).\]

Looking at an arbitrary plot of $P = \tanh I$ (taking $P_{m} = \alpha = 1$, just to look at the shape):

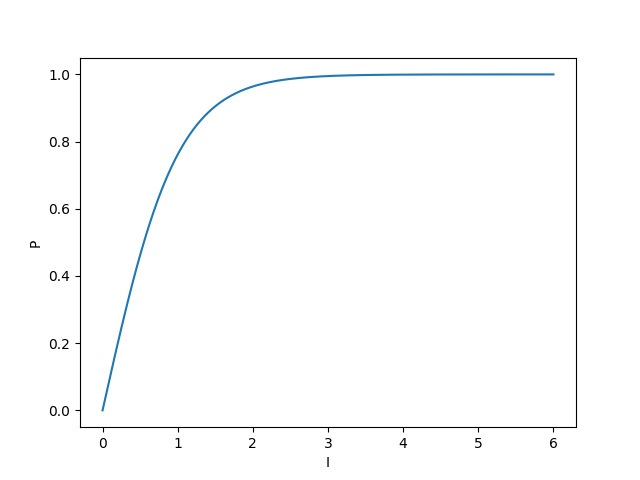
we see that it follows the first two regimes that we expect (models for photosynthetic rate against light intensity are only really concerned with the light-limited and light-saturated sections).

While this model was suggested during the 70’s and 80’s, it has not been implemented much in recent times in favour of models derived from expressions similar in form to Michaelis-Menten kinetics. Though it is a relatively simple expression to model and has been found to fit experimental data reasonably well in some studies, it has also been found to inaccurately model the light-limiting region, particularly when modelled with other key parameters, such as specific growth rate. However, the reason I wanted to write about this derivation didn’t really have much to do with the expression itself, but because of how we went from something quite ugly looking,

\[P = P_{m}\left[ \frac{\exp\left[\alpha I\left(1 - \frac{P_{m}a_{2}}{\alpha}\right)\right] - 1}{\exp\left[\alpha I \left( 1 - \frac{P_{m}a_{2}}{\alpha} \right) \right] - \left( \frac{P_{m}a_{2}}{\alpha} \right) } \right],\]

and after applying some conditions set by restrictions based on the system we’re trying to model, it collapses into a neat, little expression.

\[P = P_{m} \tanh (\alpha I).\]

Whether or not the expression has found use in modelling microalgae growth, I still think this is pretty cool.

References

Béchet , Q., Shilton, A. & Guieysse, B., 2013. Modelling the effects of light and temperature on algae growth: State of the art and critical assessment fro productivity predicition during outdoor cultivation. Biotechnology Advances, Volume 31, pp. 1648-1663.

Chalker, B. E., 1979. Modelling Light Saturation Curves for Photosynthesis: An Exponential Function. Journal of Theoretical Biology, Volume 84, pp. 205-215.

Kurano, N. & Miyachi, S., 2005. Selection of Microalgal Growth Model for Describing Specific Growth Rate-Light Response Using Extended Information Criterion. Journal of Bioscience and Bioengineering, 100(4), pp. 403-408.

Lee, E., Jalalizadeh, M. & Zhang, Q., 2015. Growth kinetic models for microalgae cultivation: A review. Algal Research, Volume 15, pp. 497-512.