A formula for pi derived from the error function.

---

In my third year at university I was introduced to the error function during a ‘Transport Phenomena’ class. It came up in the context of deriving expressions to describe heat and mass transfer through various geometries. While revising for the exam I derived an expression for $\pi$. Starting with the error function:

\[\text{erf}(z)=\frac{2}{\sqrt{\pi}}\int_{0}^{z}e^{-x^2}dx\]

Recall that the Maclaurin series of the exponential function, $e^x$, is given by

\[e^x=\sum_{n=0}^{\infty}\frac{x^n}{n!}\]

And so, we can write the error function as

\[\begin{aligned} \text{erf}(z)&=\frac{2}{\sqrt{\pi}}\int_{0}^{z}\sum_{n=0}^{\infty}\frac{(-x^2)^n}{n!}dx \\ &=\frac{2}{\sqrt{\pi}}\int_{0}^{z}\left(1-x^2+\frac{x^4}{2!}-\frac{x^6}{3!}+.\ .\ .\right)dx \end{aligned}\]

Taking the integral and applying the limits of integration gives

\[\begin{aligned} \text{erf}(z)&=\frac{2}{\sqrt{\pi}}\left[x-\frac{x^3}{3}+\frac{x^5}{5\cdot2!}-\frac{x^7}{7\cdot3!}+.\: .\: .\right]_0^z \\ &=\frac{2}{\sqrt{\pi}}\left(z-\frac{z^3}{3}+\frac{z^5}{5\cdot2!}-\frac{z^7}{7\cdot3!}+.\: .\: .\right) \\ &=\frac{2}{\sqrt{\pi}}\sum_{n=0}^{\infty}\frac{(-1)^nz^{2n+1}}{n!(2n+1)} \end{aligned}\]

Next, we consider the value of the error function at various values of $z$:

• $\text{erf}(1)\approx0.8427008$
• $\text{erf}(2)\approx0.9953223$
• $\text{erf}(3)\approx0.9999779$
• $\text{erf}(4)\approx0.9999999$

We essentially see that as $z$ increases $\text{erf}(z)$ get closer and closer to 1. And so, we can say that

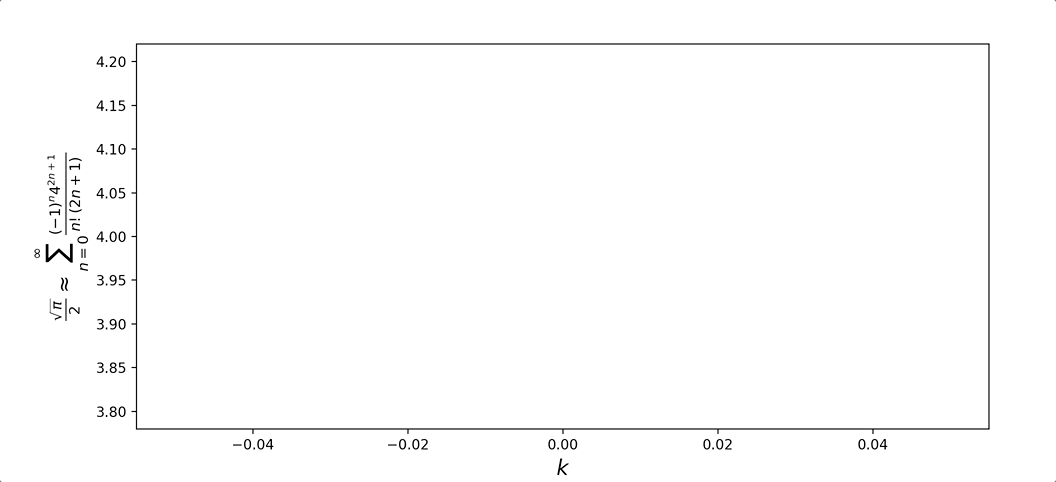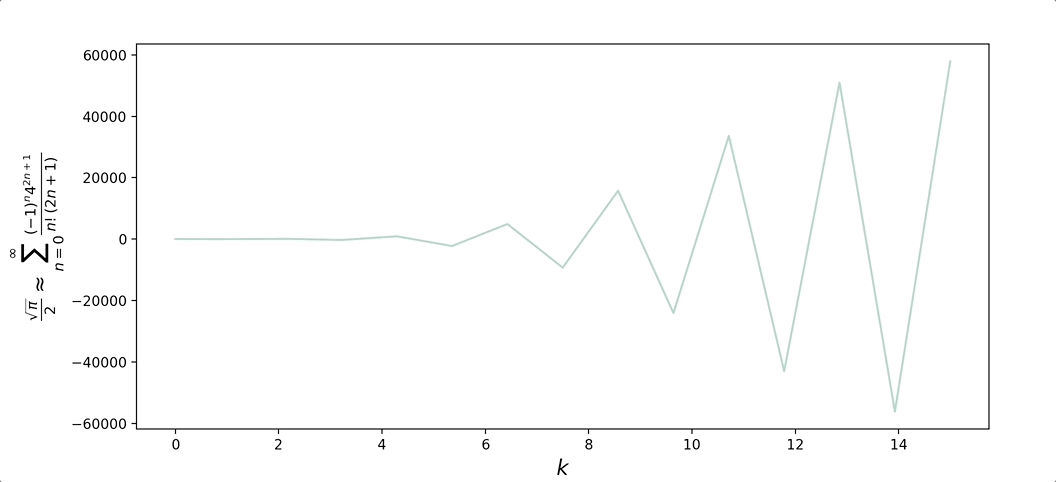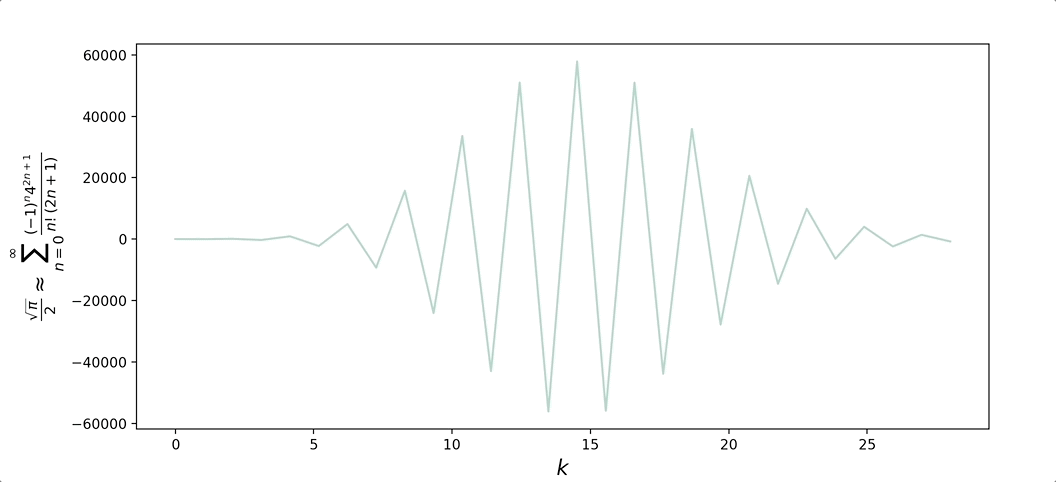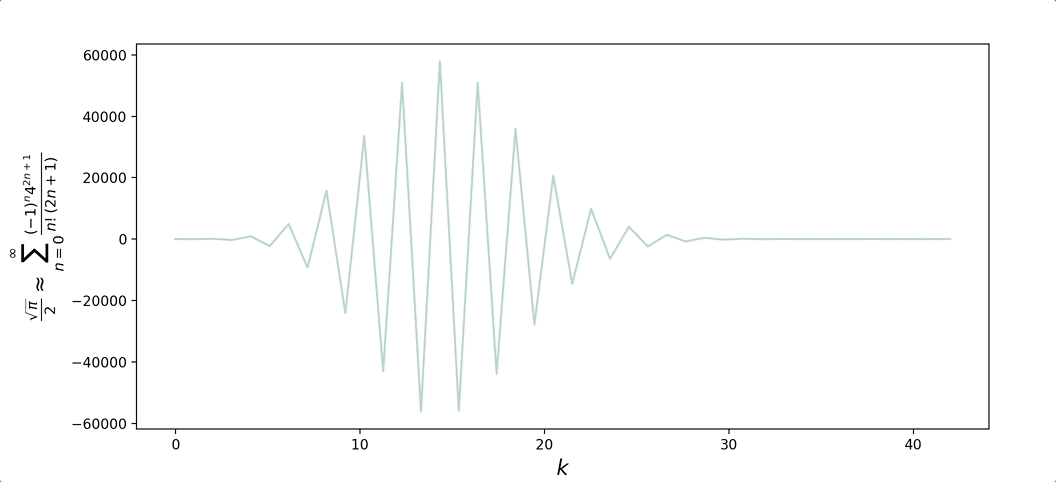
\[\begin{aligned} \lim_{z\to\infty} \text{erf}(z) &= \lim_{z\to\infty} \frac{2}{\sqrt{\pi}} \sum_{n=0}^{\infty}\frac{(-1)^nz^{2n+1}}{n!(2n+1)} = 1 \\ \frac{\sqrt{\pi}}{2} &= \lim_{z\to\infty}\sum_{n=0}^{\infty}\frac{(-1)^nz^{2n+1}}{n!(2n+1)} \end{aligned}\]

Plotting the convergence of the expression for $z = 4$, as well the expression rearranged for $\pi$: