Mass transport by diffusion

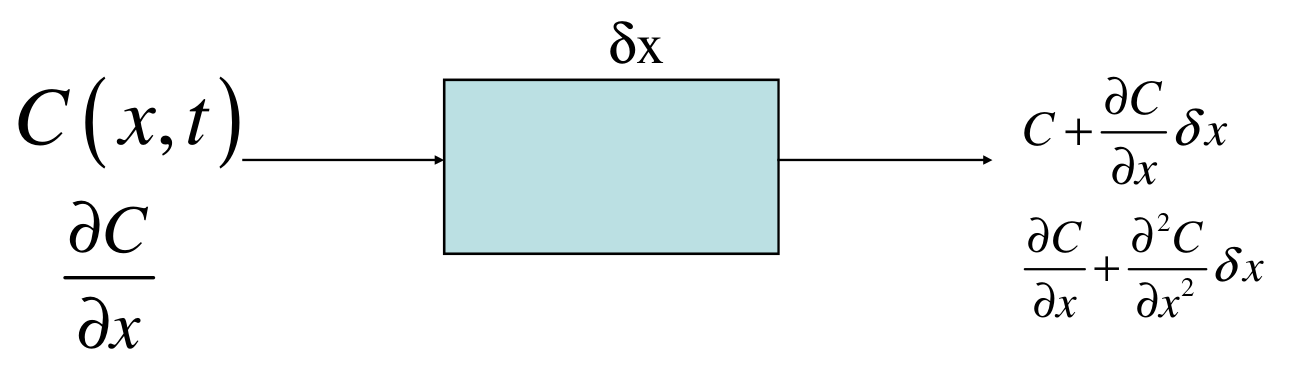
Given some medium, e.g. water, containing some material, say salt, the material will DIFFUSE from the concentrated area to the dilute area. Diffusion can be generalised by Fick’s law:

$J = -D \frac{\text{d} C}{\text{d} x}$

where $J$ is molar flux and $D$ is diffusivity. Over a small control volume and in a short period of time $\delta t$ we can perform a mass balance over the volume:

$$\text{MOLES IN} - \text{MOLES OUT} = \text{Accumulated MOLES}$$ $$-D\frac{\partial C}{\partial x} A \delta t - \left[ -D \left( \frac{\partial C}{\partial x} + \frac{\partial^2 C}{\partial x^2}\delta x \right) \right] A\delta t = V\Delta C.$$

Replacing $V = A\delta x$, and after some manipulation, we get:

$$-D\frac{\partial C}{\partial x} A \delta t - \left[ -D \left( \frac{\partial C}{\partial x} + \frac{\partial^2 C}{\partial x^2}\delta x \right) \right] A\delta t = A\delta x \Delta C.$$ $$-D\frac{\partial C}{\partial x} A \delta t + D\left( \frac{\partial C}{\partial x} + \frac{\partial^2 C}{\partial x^2}\delta x \right) A\delta t = A\delta x \Delta C.$$ $$-D\frac{\partial C}{\partial x} + D\frac{\partial C}{\partial x} + D\frac{\partial^2 C}{\partial x^2}\delta x = \delta x \frac{\Delta C}{\delta t}.$$ $$D\frac{\partial^2 C}{\partial x^2}= \frac{\Delta C}{\delta t}.$$

Taking the limit as the right hand side goes the zero we see that the above equation approaches

$$\frac{\partial C}{\partial t} = D \frac{\partial^2 C}{\partial x^2}$$

This is the 1D diffusion equation over a small control volume $V$.

Let us consider the case of transient diffusion through a semi-infinite geometry. The boundary conditions in this case are

• at $t < 0$, $C_{A} = C_{A,i},$ which is the initial molar concentration.
• at $t > 0$, $C_{A} \to C_{A,i}$ at $x = 0$.
• at $t > 0$, $C_{A} = C_{A,s}$.

Let us define a similarity variable, $\eta$, that combines the variable $x$ and $t$:

$$\eta = \frac{x}{\sqrt{4Dt}}$$

We can now re-write the diffusion equation in terms of the similarity variable.

$$\frac{\partial C}{\partial x} = \frac{\partial C}{\partial \eta}\frac{\partial \eta}{\partial x}$$ $$\frac{\partial \eta}{\partial x} = \frac{1}{\sqrt{4Dt}}$$

And so, in terms of $\eta$,

$$\frac{\partial C}{\partial x} = \frac{1}{\sqrt{4Dt}}\frac{\partial C}{\partial \eta}$$

The second derivative term can be broken up as

$$\begin{equation*} \begin{aligned} \frac{\partial^2 C}{\partial x^2} &= \frac{\partial}{\partial x}\left(\frac{\partial C}{\partial x}\right) \\ &= \frac{\partial}{\partial x}\left(\frac{\text{d} C}{\text{d} \eta}\cdot\frac{\text{d} \eta}{\text{d} x}\right) \\ &= \frac{\partial^2 C}{\partial \eta^2} \frac{\text{d}\eta}{\text{d} x}\cdot\frac{\text{d}\eta}{\text{d} x} \\ &= \frac{1}{4Dt} \frac{\partial^2 C}{\partial \eta^2} \end{aligned} \end{equation*}$$

Taking the derivative of $\eta$,

$$\begin{equation*} \begin{aligned} \frac{\partial \eta}{\partial t} &= \frac{x}{4D}\cdot\frac{-t^{-\frac{3}{2}}}{2} \\ &= -\frac{x}{2t\sqrt{4Dt}} \end{aligned} \end{equation*}$$

and so,

$$\begin{equation*} \begin{aligned} \frac{\partial C}{\partial t} &= \frac{\text{d} C}{\text{d} \eta} \frac{\text{d} \eta}{\text{d} t} \\ &= \frac{\text{d} C}{\text{d} \eta}\left(-\frac{x}{2t\sqrt{4Dt}}\right) \end{aligned} \end{equation*}$$

The diffusion equation thus becomes

$$\begin{equation*} \begin{aligned} \frac{1}{4Dt}\frac{\partial^2 C}{\partial \eta^2} &= \frac{1}{D}\frac{\text{d}C}{\text{d}\eta}\left(-\frac{x}{2t\sqrt{4Dt}}\right) \\ \frac{\text{d}^2 C}{\text{d} \eta^2} &= -\frac{2x}{\sqrt{4Dt}}\frac{\text{d}C}{\text{d}\eta} \end{aligned} \end{equation*}$$

Since $x = \eta\sqrt{4Dt}$, the above becomes

$$\begin{equation*} \begin{aligned} \frac{\text{d}^2 C}{\text{d} \eta} = -2\eta \frac{\text{d} C}{\text{d} \eta} \end{aligned} \end{equation*}$$

Rewriting the boundary conditions in terms of $\eta$ gives

• $C_{A} = C_{A, i}$ at $t = 0 \ \therefore \ \eta \to \infty$
• $C_{A} = C_{A, s}$ at $t > 0 \ \therefore \ \eta = 0$
• $C_{A} = C_{A, i}$ at $t > 0$ and as $x \to \infty \ \therefore \ \eta = 0$

The similarity variable combines the variables $x$ and $t$ into a single variable $\eta$. And so, the three boundary conditions collapse into two. In order to now solve for $C$ let $U = \frac{\text{d}C}{\text{d}\eta}$. The above equation then becomes,

$$\begin{equation*} \begin{aligned} \frac{\text{d} U}{\text{d} \eta} = - 2\eta U \end{aligned} \end{equation*}$$

and now integrating both sides,

$$\begin{equation*} \begin{aligned} \ln U &= -\eta^2 + C_0 \\ U &= C_1e^{-\eta^2} \end{aligned} \end{equation*}$$

Substituting back in for $U$ we can solve for $C$.

$$\begin{equation*} \begin{aligned} \frac{\text{d} C}{\text{d} \eta} &= C_1e^{-\eta^2} \\ C &= C_1\int e^{-\eta^2} \text{d}\eta + C_2 \end{aligned} \end{equation*}$$

Applying the boundary conditions:

• $C(\eta = 0) = C_s \Rightarrow C_2 = C_s$
• $C(\eta \to \infty) = C_i \Rightarrow C_i = C_1\int_0^\infty e^{-\eta^2} \text{d} \eta + C_s$

The above integral is half the Gaussian integral which can be evaluated to $\frac{\sqrt{\pi}}{2}$ (see this post and the resources and the end to see why this is the case). We can, therefore, find the value of $C_1$:

$$\begin{equation*} \begin{aligned} C_i = \frac{\sqrt{\pi}}{2}C_1 + C_s \\ C_1 = \frac{2}{\sqrt{\pi}}(C_i - C_s) \end{aligned} \end{equation*}$$

And so, we get the expression for $C$:

$$\begin{equation*} \begin{aligned} C = \frac{2}{\sqrt{\pi}}(C_i - C_s)&\int_0^\eta e^{-\eta^2} \text{d} \eta + C_s \\ \frac{C - C_s}{C_i - C_s} = \frac{2}{\sqrt{\pi}}&\int_0^\eta e^{-\eta^2}\text{d}\eta \end{aligned} \end{equation*}$$

The integral $\int_0^\eta e^{-\eta^2} \text{d} \eta$ cannot be solved analytically (except for $\eta \to \infty$), however, it can be solved numerically. The error function can be defined as

$$\begin{equation*} \begin{aligned} \text{erf}(\eta) \equiv \frac{2}{\sqrt{\pi}} \int_0^\eta e^{-\eta^2} \text{d} \eta \end{aligned} \end{equation*}$$

with $\text{erf}(1) = 1$ and $\text{erf}(0) = 0$. And so, we get the expression for the concentration profile for semi-transient diffusion through a semi-infinite geometry,

$$\begin{equation*} \begin{aligned} \boxed{ \frac{C - C_s}{C_i - C_s} = \text{erf}(\eta) } \end{aligned} \end{equation*}$$